Derivatives Crisis Of Banks…Worldwide

“Derivatives are weapons of mass destruction” – Warren Buffett

The What And Why Of Derivatives

"Megabanks trade risk via derivatives contracts to another firm while keeping the underlying asset on their books. This way they can bypass capital requirements and take on more debt. This, in turn, allows them to make more trades, but it also means that if a sudden downturn surfaces in the markets, the firm which borrowed way beyond their means may quickly go bankrupt. Lehman Brothers experienced this after they’d borrowed 30 times more money than they had in reserve. In that case, a relatively small loss of a mere 3% meant that Lehman no longer had reserves (i.e. capital), and they therefore collapsed…i.e. totally wiped out. The leverage that derivatives allow is incomprehensible. They are betting 30 TIMES MORE MONEY THAN THEY HAVE. This is financially insane." (Source:  http://www.huffingtonpost.ca/nick-fillmore/banks-derivatives_b_4408856.html )

Who was Lehman Brothers…and what happened to them?

Lehman Brothers had humble origins, tracing its roots back to a small general store that was founded by German immigrant Henry Lehman in Montgomery, Alabama in 1844. In 1850, Henry Lehman and his brothers, Emanuel, and Mayer, founded Lehman Brothers.

While the firm prospered over the following decades as the US economy grew into an international powerhouse, Lehman had to contend with plenty of challenges over the years. Lehman survived them all – the railroad bankruptcies of the 1800s, the Great Depression of the 1930s, two world wars, a capital shortage when it was spun off by American Express Co. (AXP) in 1994, and the Long Term Capital Management collapse and Russian debt default of 1998. However, despite its ability to survive past disasters, the collapse of the U.S. housing market ultimately brought Lehman Brothers to its knees, as its headlong rush into the subprime mortgage market proved to be a disastrous step.

On September 15, 2008, Lehman Brothers filed for bankruptcy. With $639 billion in assets and $619 billion in debt, Lehman's bankruptcy filing was the largest in history, as its assets far surpassed those of previous bankrupt giants such as WorldCom and Enron. Lehman was the fourth-largest US investment bank at the time of its collapse with 25,000 employees worldwide.

The world’s largest financial institutions trade derivatives. Derivatives are instruments that derive their value from fluctuations in the price of an underlying asset such as a stock or a commodity. Financial institutions, asset managers, corporations, and governments use derivatives to manage volatility in assets that their respective enterprises are exposed to. At the time of its bankruptcy, Lehman Brothers had an estimated $35 trillion notional derivatives portfolio.

From 2004-2007 Lehman Brothers and Deutsche Bank (DB) were indeed riding high on the global financial hog.  They were literally gorging themselves via Derivative Exposure…ad nauseam.  Then the proverbial poop hit the fan as both Lehman Brothers and Deutsche Bank were hemorrhaging on insane ingestion of many Trillions of Dollars in DERIVATIVES. Subsequently, Lehman Brothers went belly up…with its stock price going into freefall from $25/share in 2007 to a mere 10 cents/share by early 2009.  Moreover, Lehman Brothers shares are today only 12 cents a share.  Likewise, Deutsche Bank’s catastrophic derivative exposure has hammered down its stock price from $135 in 2007 to only $17/share today…ergo a heart-stopping price loss of -87%. Furthermore, DB’s stock price appears to be hell bent for leather to follow Lehman Brothers’ lethal path to Wall Street’s graveyard…due primarily to its oppressive Derivative’s Exposure.  See Chart below:

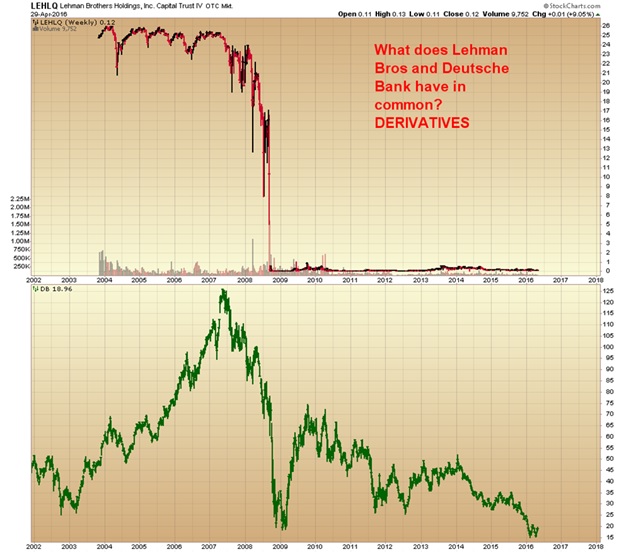
Interesting Historical Note:  When Lehman Brothers failed, it had $35 Trillion in Derivative Exposure. Now compare this with today’s Deutsche Bank Derivative Exposure of a cardiac-arrest $75 Trillion in DERIVATIVES…and you will understand WHY DB share value is relentlessly and methodically falling in recent years. In fact, today May 3rd, Deutsche Bank stock has already been hammered down more than 6% in today’ early hours of New York trading.

Indeed:  “Derivatives are weapons of mass destruction” – Warren Buffett

What is the global magnitude of these financial weapons of mass destruction?

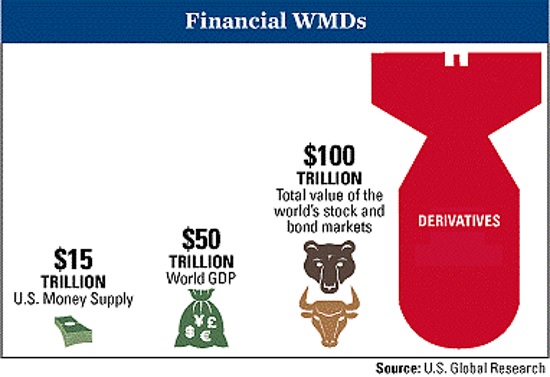
Global Derivatives: $1.5 Quadrillion Time Bomb

That’s $1,500,000,000,000,000…equivalent to nearly $200,000 per every man, woman and child on this earth !!

(Source:  http://www.globalresearch.ca/global-derivatives-1-5-quadrillion-time-bomb/5464666  )

The legendary Lehman Brothers financial dynasty is dead and buried in Wall Street’s cemetery. However, Germany’s giant financial power house – Deutsche Bank is today vying helter-skelter to duplicate the infamous legacy of the tragic Lehman Brothers saga.

Is It Time To Panic About Deutsche Bank?

"At $72.8 Trillion, The Bank With The Biggest Derivative Exposure In The World" was not JPMorgan as some had expected, but Germany's banking behemoth, Deutsche bank.

Financial Armageddon Approaches: US Banks Have 247 Trillion Dollars Of Exposure To Derivatives

The following US bank numbers reveal a self-destructing recklessness that is on a level that is near criminal negligence.

Citigroup: Total Assets more than 1.8 trillion dollars

Total Derivatives more than 53 trillion dollars

JPMorgan Chase: Total Assets about 2.4 trillion dollars)

Total Derivatives more than 51 trillion dollars)

Goldman Sachs: Total Assets less than a trillion dollars

Total Derivatives more than 51 trillion dollars

Bank Of America:  Total Assets a little bit more than 2.1 trillion dollars

Total Derivatives more than 45 trillion dollars

Morgan Stanley: Total Assets less than a trillion dollars

Total Derivatives more than 31 trillion dollars

Wells Fargo:  Total Assets more than 1.7 trillion dollars

Total Derivatives more than 6 trillion dollars

Today six major US banks are betting 24 TIMES MORE MONEY THAN THEY HAVE (i.e. $237 Trillion in Total Derivatives vs only $10 Trillion in Total Assets).  Even more insanely lethal is the Derivative exposure of Deutsche Bank, which has $75 Trillion vis-à-vis Total Assets of a mere $1.6 Trillion.  Sadly DB is betting nearly 47 TIMES MORE MONEY THAN THEY HAVE (astoundingly, it’s the biggest Derivatives Exposure in the world). Clearly, it’s insanely suicidal. (Source: http://www.zerohedge.com/news/2016-02-03/it-time-panic-about-deutsche-bank)

This is financially crazy for the following reason. In a hypothetical case where a relatively small Derivatives Investment Loss of a mere 4% would mean that six major US banks might be totally wiped out. The leverage that derivatives permit is incomprehensible…ludicrously suicidal! It’s even worse for Deutsche Bank, where a Derivative Investment Loss of less than 3% would crash DB into immediate bankruptcy…a la Lehman Brothers.

To be sure, this is Financial Armageddon to the Nth degree.

The dire warning words of Warren Buffett are gospel:  “Derivatives are weapons of mass destruction”

******** 

Related Articles

Deutsche Bank Is Crashing Again as European Banks Slide to Crisis Lows

US Treasuries Will Sink Into A Black Hole

Derivatives: The Unregulated Global Casino for Banks

********